지금까지의 신경망 - 피드포워드 (feed forward) 신경망
-> 시계열 데이터 다루지 못한다는 단점
=> 순환 신경망 RNN 등장
5.1 확률과 언어 모델
5.1.1 word2vec을 확률 관점에서 바라보다
- 지금까지는 맥락을 좌우 대칭으로 생각해옴
-> 맥락을 왼쪽 윈도우만으로 한정


5.1.2 언어 모델
- 단어 나열에 확률 부여
- 특정한 단어의 시퀀스에 대해 그 시퀀스가 일어날 가능성을 확률로 평가
- 수식적 설명
- W1,...,Wm이라는 m개 단어로 된 문장
- 단어 W1,...,Wm이라는 순서로 출현할 확률 : P(W1,...,Wm) -> 동시 확률 (여러 사건이 동시에 일어날 확률)
- 사후 확률을 사용하여 분해 가능 (확률의 곱셈정리에 의해)
- 파이 기호 : 모든 원소를 곱하는 총곱

-> 사후확률 : 타깃 단어보다 왼쪽에 있는 모든 단어를 맥락(조건)으로 했을 때의 확률
=> 조건부 언어 모델
5.1.3 CBOW 모델을 언어 모델로?
- word2vec의 CBOW모델을 언어 모델에 적용
- 맥락 크기를 특정 값으로 한정하여 근사적으로 나타냄
- 맥락을 왼쪽 2개의 단어로 한정

-> 맥락 2개의 단어 => 2층 마르코프 연쇄
(마르코프 연쇄 : 미래의 상태가 현재 상태에만 의존해 결정, N개의 사건에 의존 - N층 마르코프 연쇄)
- 맥락 크기 임의 길이로 설정 가능
-> 특정 길이로 고정 => 맥락보다 더 왼쪽에 있는 단어의 정보는 무시됨
- 맥락 크기를 키워도 맥락 안의 단어 순서가 무시된다는 한계

- 왼쪽 : 단어 벡터들이 더해지므로 맥락의 단어 순서 무시됨
- 오른쪽 : 단어 벡터를 은닉층에서 연결 (concatenate)
-> 가중치 매개변수 늘어남
=> RNN - 맥락이 아무리 길더라도 그 맥락의 정보를 기억하는 메커니즘을 갖춤
5.2 RNN이란
: 순환하는 신경망
(재귀 신경망과 다름)
5.2.1 순환하는 신경망
- 순환 의미
- 한 지점에서 시작한 것이, 시간을 지나 다시 원래 장소로 돌아오는 것, 그리고 이 과정을 반복
- 닫힌 경로 혹은 순환하는 경로가 존재해야 순환 가능

- Xt는 벡터라고 가정
- t : 시각
- 각 단어의 분산 표현(단어 벡터) : Xt -> 순서대로 RNN계층에 입력
5.2.2 순한 구조 펼치기
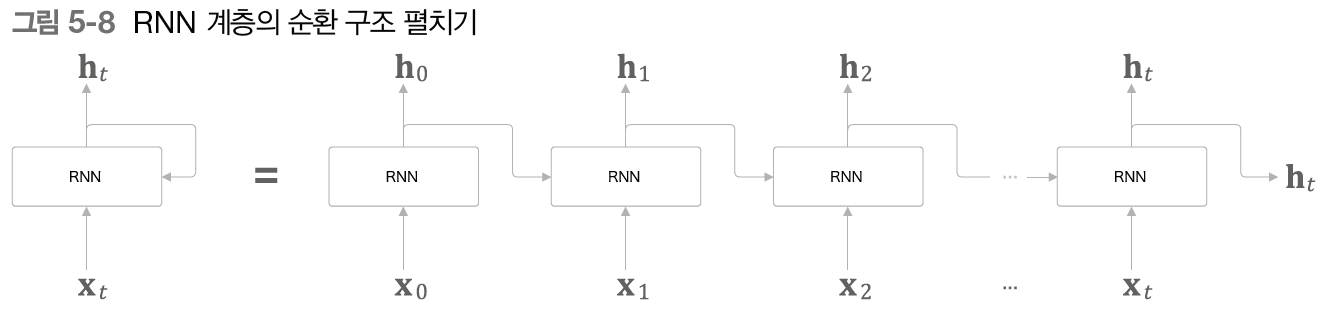
- 각 시각의 RNN계층은 그 계층으로의 입력과 1개 전의 RNN계층으로부터의 출력을 받음
- 두 정보를 바탕으로 현 시각의 출력을 계산

- 가중치 2개
- Wx : 입력 x를 출력 h로 변환하기 위한 가중치
- Wh : 1개의 RNN출력을 다음 시각의 출력으로 변환하기 위한 가중치
- 편항 b
- 행렬 곱 계산하고 그 합을 tanh함수(쌍곡탄젠트hyperbolic tangent 함수)를 이용해 변환
- ht는 다른 계층을 향해 출력되는 동시에, 다음 시각의 RNN 계층을 향해도 출력
- 현재의 출력은 한 시각 이전 출력에 기초해 계산
- RNN은 h라는 상태를 가지고 있으며 시각이 1단위 진행될 때마다 갱신되는 것
- RNN 계층 : 상태를 가지는 계층, 메모리(기억력)가 있는 계층
- ht : 은닉 상태 (은닉 상태 벡터)
5.2.3 BPTT

- RNN의 오차역전파법 - 시간 방향으로 펼친 신경망의 오차역전파법 BPTT(backpropagation through time)
-> 긴 시계열 데이터를 학습할 때의 문제
- 시간 크기가 커지는 것에 비례하여 소비하는 컴퓨팅 자원 증가, 기울기 불안정
5.2.4 Truncated BPTT
- 적당한 지점에서 잘라내어 작은 신경망 여러 개로 만듦
- 잘라낸 작은 신경망에서 오차역전파법 수행
-> Truncated BPTT (잘라낸 오차역전파법)
- 순전파 연결은 그대로 유지
- 역전파의 연결은 잘라내고 잘라낸 단위로 학습 수행
- 데이터를 순서대로 입력해야 함

-> 블록 단위로 오차역전파법 적용
5.2.5 Truncated BPTT의 미니배치 학습
- 데이터 시작 위치를 각 미니배치의 시작 위치로 옮겨줌

- 첫번째 미니배치 원소 : X0~X9 두번째 미니배치 원소 : X500~X509
-> X10~X19 X510~X519
5.3 RNN 구현

- 한 단계의 작업을 수행하는 계층 : RNN 계층
- T개 단계분의 작업을 한꺼번에 처리하는 계층 : Time RNN 계층
5.3.1 RNN 계층 구현


- N : 미니배치 크기
- D : 입력 벡터의 차원 수
- H : 은닉 상태 벡터의 차원 수

class RNN:
def __init__(self, Wx, Wh, b):
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.cache = None
def forward(self, x, h_prev): #순전파
Wx, Wh, b = self.params
t = np.matmul(h_prev, Wh) +np.matmul(x, Wx)+b
h_next = np.tanh(t)
self.cashe = (x, h_prev, h_next)
return h_next
def backward(self, dh_next):
dt = dh_next*(1-h_next**2)
db = np.sum(dt, axis=0)
dWh = np.matmul(h_prev.T, dt)
dh_prev = np.matmul(dt, Wh.T)
dWx = np.matmul(x.T, dt)
dx = np.matmul(dt, Wx.T)
self.grads[0][...] = dWx
self.grads[1][...] = dWh
self.grads[2][...] = db
return dx, dh_prev
5.3.2 Time RNN 계층 구현
: T개의 RNN 계층으로 구성



class TimeRNN:
def __init__(self, Wx, Wh, b, stateful=False): #stateful : 은닉 상태 유지(순전파 끊지 않고 전파) 결정 인수
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.layers = None #다수의 RNN계층 리스트로 저장
self.h, self.dh = None, None
#h : forward()메서드를 불렀을 때의 마지막 RNN계층의 은닉 상태 저장
#dh : backward()메서드를 불렀을 때 하나 앞 블록의 은닉 상태의 기울기 저장
self.stateful = stateful
def set_state(self, h):
self.h = h
def reset_state(self):
self.h = None
def forward(self, xs): #순전파
Wx, Wh, b = self.params
N, T, D = xs.shape #미니배치 크기 : N, T개 분량의 시계열 데이터, 입력 벡터의 차원 수 : D
D, H = Wx.shape
self.layers=[]
hs = np.empty((N, T, H), dtype='f') #출력값 담을 그릇
if not self.stateful or self.h is None: #stateful이 false이거나 처음 호출 시
self.h = np.zeros((N, H), dtype='f') #0행렬로 초기화
for t in range(T): #T회의 RNN계층 생성
layer = RNN(*self.params)
self.h = layer.forward(xs[:, t, :], self.h) #h_next
hs[:, t, :] = self.h
self.layers.append(layer)
return hs
def backward(self, dhs):
Wx, Wh, b = self.params
N, T, H = dhs.shape
D, H = Wx.shape
dxs = np.empty((N, T, D), dtype='f') #하류로 흘려보낼 기울기를 담을 그릇
dh = 0
grads = [0,0,0]
for t in reversed(range(T)):
layer =self.layers[t]
dx, dh = layer.backward(dhs[:, t, :]+dh) #합산된 기울기
#RNN의 순전파에서는 출력이 2개로 분기 (ht, ht_next) -> 역전파 시 (dht +dh_next)가 입력
dxs[:, t, :] = dx
for i, grad in enumerate(layer.grads): #각 RNN계층의 가중치 기울기 합산
grads[i] += grad
for i, grad in enumerate(grads):
self.grads[i][...] = grad
self.dh = dh
return dxs5.4 시계열 데이터 처리 계층 구현
RNN을 사용한 언어 모델 : RNNLM
5.4.1 RNNLM의 전체 그림

- Embedding계층 : 단어 ID를 단어의 분산 표현으로 변환
- RNN 계층 : 은닉 상태를 다음 층(Affine)으로 출력함과 동시에 다음 시각의 RNN계층으로 출력
- Affine계층을 거쳐 Softmax 계층으로 전해짐
- 맥락을 기억하고 있음 (과거의 정보를 응집된 은닉 상태 벡터로 저장)
5.4.2 Time 계층 구현

- T개의 Embedding 계층
- T개의 Affine 계층
- T개의 softmax with loss 손실을 합산해 평균한 값이 최종 손실
5.5 RNNLM 학습과 평가
5.5.1 RNNLM 구현

from common.time_layers import *
class SimpleRnnlm:
def __init__(self, vocab_size, wordvec_size, hidden_size):
V, D, H = vocab_size, wordvec_size, hidden_size
rn = np.random.randn
#가중치 초기화
embed_W = (rn(V, D)/100).astype('f')
rnn_Wx = (rn(D, H)/ np.sqrt(D)).astype('f') #Xavier초깃값 이용
rnn_Wh = (rn(H, H)/ np.sqrt(H)).astype('f')
rnn_b = np.zeros(H).astype('f')
affine_W = (rn(H, V)/ np.sqrt(H)).astype('f')
affine_b = np.zeros(V).astype('f')
#계층 생성
self.layers = [
TimeEmbedding(embed_W),
TimeRNN(rnn_Wx, rnn_Wh, rnn_b, stateful=True),
TimeAffine(affine_W, affine_b)
]
self.loss_layer = TimeSoftmaxWithLoss()
self.rnn_layer = self.layers[1]
#모든 가중치와 기울기를 리스트에 모은다.
self.params, self.grads = [], []
for layer in self.layers:
self.params +=layer.params
self.grads += layer.grads
def forward (self, xs, ts):
for layer in self.layers:
xs = layer.forward(xs)
loss = self.loss_layer.forward(xs, ts)
return loss
def backward (self, dout=1):
dout = self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return dout
def reset_state(self):
self.rnn_layer.reset_state()- RNN계층과 Affine 계층에서 Xavier 초깃값 이용
- Xavier 초깃값 : 이전 계층의 노드가 n개라면 표준편차가 1/루트n인 분포로 값들을 초기화
- 표준편차 : 데이터의 차이를 직관적으로 나타내는 척도
5.5.2 언어 모델의 평가
- 퍼플렉서티 (perplexity : 혼란도) 이용
- 확률의 역수
- 예) you 다음에 나올 단어로 say 0.8의 확률로 예측 -> 1/0.8 = 1.25
- 작을수록 좋음
- 분기 수로 해석
- 분기 수 : 다음에 취할 수 있는 선택사항의 수
- 예) 분기수 =1.25 -> 다음에 출현할 수 있는 단어의 후보를 1개 정도로 좁힘
=> 입력 데이터가 여러개

- L : 신경망의 손실
5.5.3 RNNLM의 학습 코드
import matplotlib.pyplot as plt
from common.optimizer import SGD
from dataset import ptb
#하이퍼파라미터 설정
batch_size = 10
wordvec_size = 100
hidden_size = 100 #RNN의 은닉 상태 벡터의 원소 수
time_size = 5 #Truncated BPTT가 한번에 펼치는 시간 크기
lr = 0.1
max_epoch = 100
#학습데이터 읽기 (전체 중 1000개만)
corpus, word_to_id, id_to_word = ptb.load_data('train')
corpus_size = 1000
corpus = corpus[:corpus_size]
vocab_size = int(max(corpus)+1)
xs = corpus[:-1] #입력
ts = corpus[1:] #출력 (정답 레이블)
data_size = len(xs)
print( '말뭉치 크기:%d, 어휘 수 : %d' %(corpus_size, vocab_size))
#학습 시 사용하는 변수
max_iters = data_size // (batch_size * time_size)
time_idx = 0
total_loss = 0
loss_count = 0
ppl_list = []
#모델 생성
model = SimpleRnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)
#1. 각 미니배치에서 샘플을 읽기 시작 위치를 계산
jump= (corpus_size -1) // batch_size
offsets = [i*jump for i in range(batch_size)]
for epoch in range(max_epoch):
for iter in range(max_iters):
#2. 미니배치 획득
batch_x = np.empty((batch_size, time_size), dtype='i')
batch_t = np.empty((batch_size, time_size), dtype='i')
for t in range(time_size):
for i, offset in enumerate(offsets):
batch_x[i, t] = xs[(offset +time_idx)%data_size] #각 미니배치
batch_t[i, t] = ts[(offset +time_idx)%data_size]
time_idx +=1
#기울기를 구하여 매개변수 갱신
loss = model.forward(batch_x, batch_t)
model.backward()
optimizer.update(model.params, model.grads)
total_loss += loss
loss_count +=1
#3. 에폭마다 퍼플렉서티 평가
ppl = np.exp(total_loss/loss_count) #에폭마다 손실 평균 구하고 퍼플렉서티 구함
print('|에폭 %d | 퍼플렉서티 %.2f' %(epoch+1, ppl))
ppl_list.append(float(ppl))
total_loss, loss_count = 0,0
# 그래프 그리기
x = np.arange(len(ppl_list))
plt.plot(x, ppl_list, label='train')
plt.xlabel('epochs')
plt.ylabel('perplexity')
plt.show()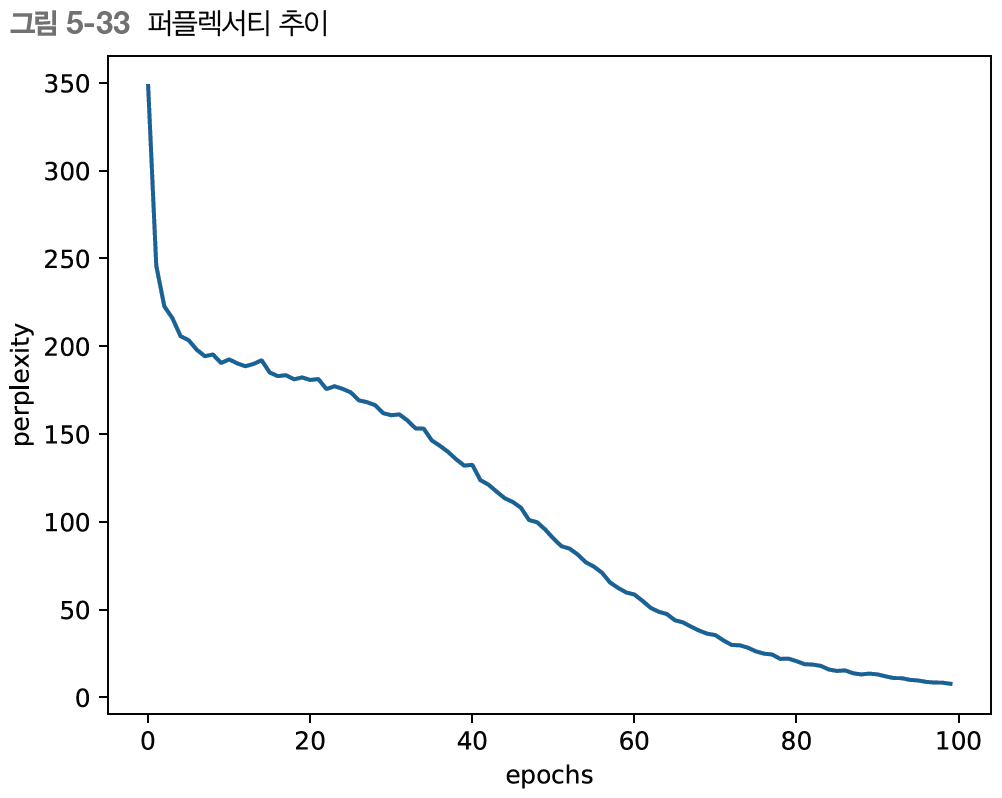

책 : 300 넘던 값 -> 최솟값인 1에 근접
나 : 에폭 1 | 퍼플렉서티 405.78 -> 에폭 100 | 퍼플렉서티 5.86
5.5.4 RNNLM 의 Trainer 클래스
앞 절의 학습 코드를 RnnlmTrainer 클래스를 사용해 다시 씀
# 하이퍼파라미터 설정
batch_size = 10
wordvec_size = 100
hidden_size = 100 # RNN의 은닉 상태 벡터의 원소 수
time_size = 5 # RNN을 펼치는 크기
lr = 0.1
max_epoch = 100
# 학습 데이터 읽기
corpus, word_to_id, id_to_word = ptb.load_data('train')
corpus_size = 1000 # 테스트 데이터셋을 작게 설정
corpus = corpus[:corpus_size]
vocab_size = int(max(corpus) + 1)
xs = corpus[:-1] # 입력
ts = corpus[1:] # 출력(정답 레이블)
# 모델 생성
model = SimpleRnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)
trainer = RnnlmTrainer(model, optimizer)
trainer.fit(xs, ts, max_epoch, batch_size, time_size) #학습 수행
#1.미니배치 순차적으로 만들어
#2.모델의 순전파와 역전파를 호출
#3.옵티마이저로 가중치를 갱신하고
#4.퍼플렉서티를 구함
trainer.plot()5.6 정리
- RNN은 순환하는 경로가 있고, 이를 통해 내부에 은닉 상태를 기억할 수 있다.
- RNN의 순환 경로를 펼침으로써 다수의 RNN 계층이 연결된 신경망으로 해설할 수 있으며, 보통의 오차역전파법으로 학습할 수 있다.(=BPTT)
- 긴 시계열 데이터를 학습할 때는 데이터를 적당한 길이씩 모으고(블록), 블록 단위로 BPTT에 의한 학습을 수행한다.(=Truncated BPTT)
- Truncated BPTT에서는 역전파의 연결만 끊는다.
- Trncated BPTT에서는 순전파의 연결을 유지하기 위해 데이터를 순차적으로 입력해야 한다.
- 언어 모델은 단어 시퀀스를 확률로 해석한다.
- RNN계층을 이용한 조건부 언어 모델은 그때까지 등장한 모든 단어의 정보를 기억할 수 있다.
책 참고 : 밑바닥부터 시작하는 딥러닝 (한빛미디어)
'딥러닝 > 밑바닥부터 시작하는 딥러닝 2' 카테고리의 다른 글
| 7장 : RNN을 사용한 문장 생성 (2) | 2023.09.27 |
|---|---|
| 6장 : 게이트가 추가된 RNN (0) | 2023.09.26 |
| 4장 : word2vec 속도 개선 (0) | 2023.09.23 |
| 3장 : word2vec (0) | 2023.09.21 |
| 2장 : 자연어와 단어의 분산 표현 (2) | 2023.09.21 |



