추론 기반 기법
3.1 추론 기반 기법과 신경망
단어를 벡터로 표현하는 방법 - 통계 기반 기법, 추론 기반 기법 -> 모두 분포 가설이 배경
3.1.1 통계 기반 기법의 문제점
- 대규모 말뭉치를 다룰 때 문제 발생
- SVD를 nxn 행렬에 적용하는 비용은 O(n^3)
- 통계 기반 기법은 1회의 처리만에 단어의 분산 표현 얻음
- 추론 기반 기법에서는 신경망을 이용해 미니배치로 학습 -> 학습 샘플씩 반복해서 학습하며 가중치 갱신
-> 계산량이 큰 작업 처리 가능, GPU 이용한 병렬 계산 가능
3.1.2 추론 기반 기법 개요
추론 : 주변 단어(맥락)가 주어졌을 때 ?에 무슨 단어가 들어가는지 추측하는 작업

- 추론 문제를 반복해서 풀면서 단어의 출현 패턴 학습
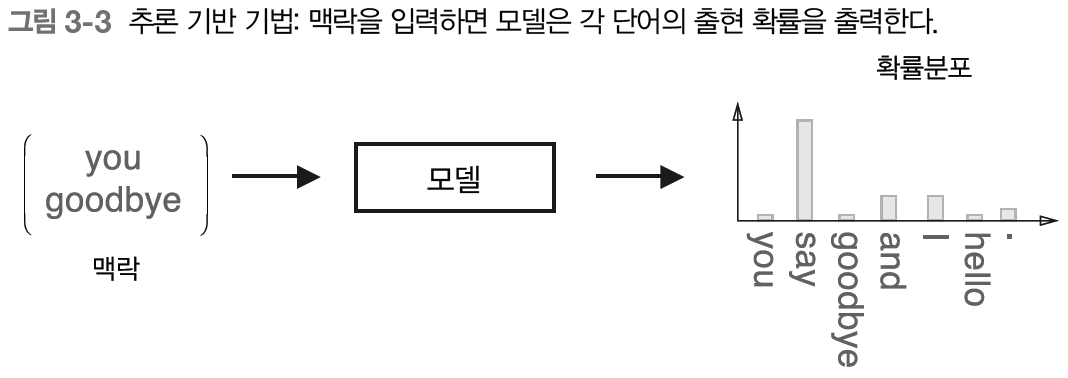
- 모델 - 맥락 정보를 입력받아 각 단어의 출현 확률을 출력
- 말뭉치를 사용해 모델이 올바른 추측을 내놓도록 학습
3.1.3 신경망에서의 단어 처리
- 단어를 고정길이의 벡터로 변환
- 원핫 표현 (원핫 벡터) 사용
- 원핫 표현 : 벡터의 원소 중 하나만 1이고 나머지는 모두 0인 벡터
- 총 어휘 수만큼의 원소를 갖는 벡터 준비 -> 인덱서가 단어 ID와 같은 원소를 1로, 나머지는 모두 0으로 설정
- 뉴런의 수 고정 가능 (그림에서 7개)


- 완전연결계층이므로 각각의 노드가 이웃 층의 모든 노드와 화살표로 연결
- 이번 장의 완전연결계층에서는 편향 생략

##완전연결계층에 의한 단어 벡터 변환
c = np.array([[1,0,0,0,0,0,0]]) #입력
W = np.random.randn(7,3) #가중치
h = np.matmul(c, W) #중간 노드
print(h)
##방법2 - Matmul 계층으로 수행
c = np.array([[1,0,0,0,0,0,0]])
layer = MatMul(W)
h = layer.forward(c) #순전파 수행
print(h)->
[[-1.43238709 0.23664779 -1.40858452]]
[[-1.43238709 0.23664779 -1.40858452]]
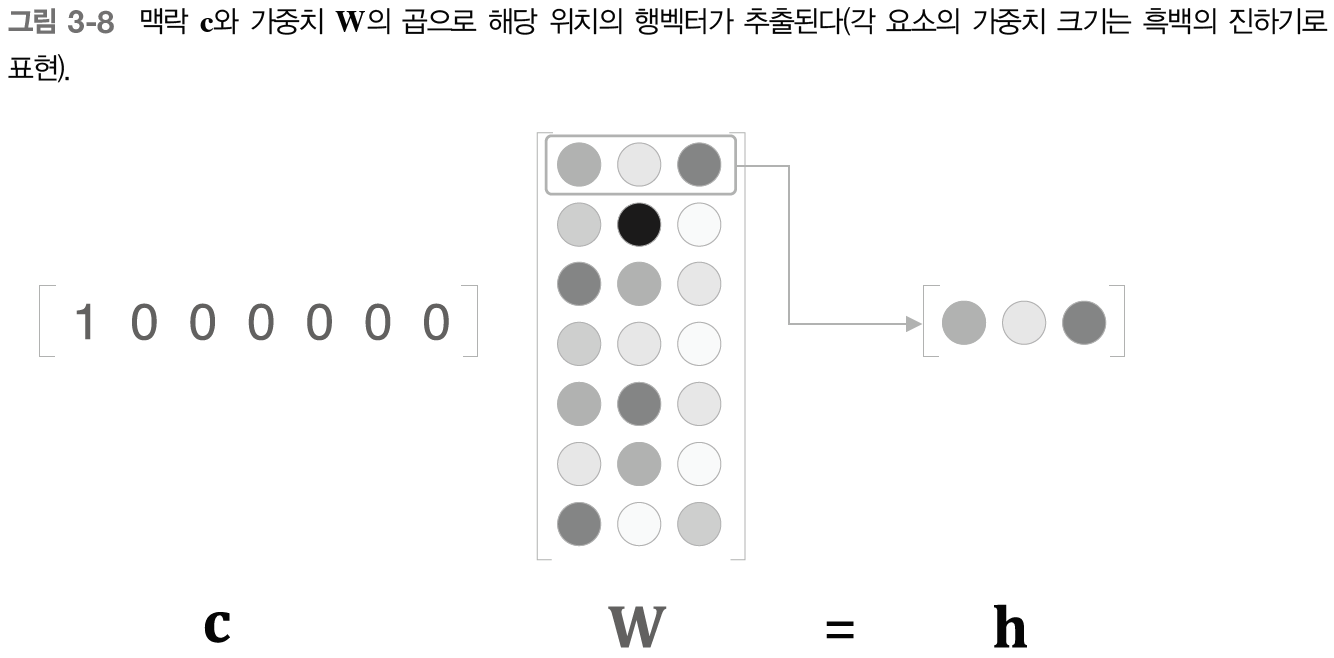
- 단어ID가 0인 단어를 원핫표현으로 표현한 다음 완전연결계층 통과시켜 변환
- c와 W의 행렬 곱 부분에서 c는 원핫 표현이기 때문에 행렬 곱은 결국 가중치의 행벡터 하나를 뽑아낸 것과 같음
3.2 단순한 word2vec
word2vec에서 사용하는 신경망
- CBOW 모델 (continuous bag-of-words)
- skip-gram 모델
3.2.1 CBOW 모델의 추론 처리
CBOW 모델 : 맥락으로부터 타깃을 추측하는 용도의 신경망
- 입력은 맥락
- 맥락 : 단어들의 목록 ("you", "goodbye")
- 맥락을 원핫 표현으로 변환
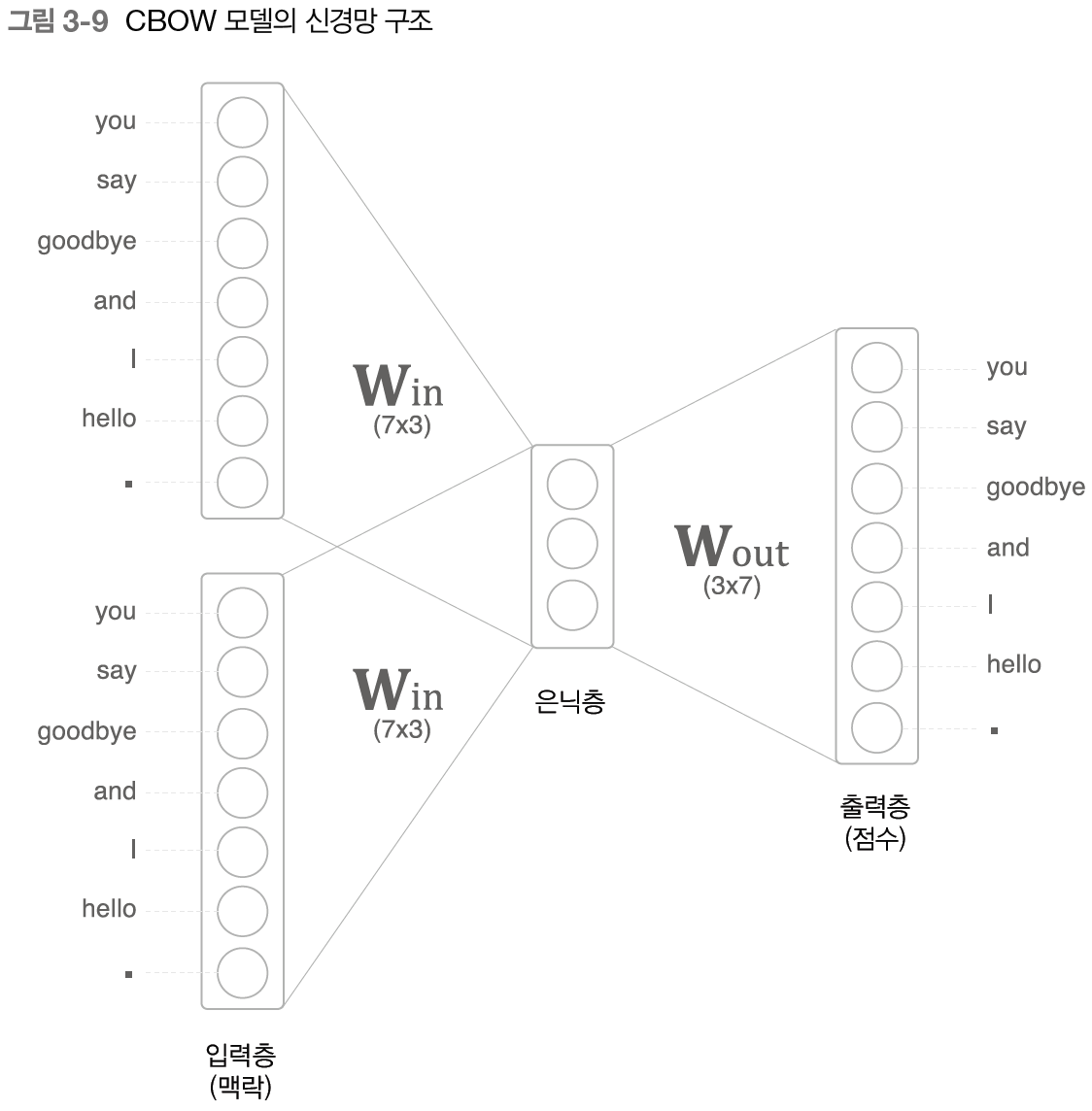
- 입력층 2개 (맥락으로 고려할 단어를 2개로 정했기 때문, N개라면 입력층도 N개)
- 은닉층을 거쳐 출력층에 도달
- 입력층에서 은닉층으로의 변환은 똑같은 완전연결계층 (가중치 Win)이 처리
- 은닉층에서 출력층 뉴런으로의 변환은 다른 완전연결계층 (가중치 Wout)이 처리
- 은닉층의 뉴런은 입력층의 완전연결계층에 의해 변환된 값
입력층이 여러 개이면 전체를 평균 1/2(h1 +h2) - 출력층의 뉴런 하나하나는 각 단어에 대응
-> 출력층 뉴런 : 각 단어의 점수
=> 값이 높을수록 대응 단어의 출현 확률도 높아짐 (확률은 점수를 소프트맥스 함수를 적용해 얻음) - 은닉층의 뉴런 수를 입력층의 뉴런 수보다 적게 하는 것이 핵심
-> 은닉층에는 필요한 정보를 간결하게 담게 됨 -> 밀집벡터 표현 얻을 수 있음 - 은닉층의 정보는 인간이 이해할 수 없는 코드로 쓰여 있음 : 인코딩
- 은닉층의 정보로부터 원하는 결과를 얻는 작업 : 디코딩

- 완전연결계층의 가중치 Win (7x3)
- 단어의 분산 표현의 정체
- 각 행에는 해당 단어의 분산 표현이 담겨 있음
- 학습을 진행할수록 분산 표현들이 갱신됨
- 단어의 의미도 녹아들어 있음

##CBOW모델의 추론 처리
#샘플 맥락 데이터
c0 = np.array([[1,0,0,0,0,0,0]])
c1 = np.array([[0,0,1,0,0,0,0]])
#가중치 초기화
W_in = np.random.randn(7,3)
W_out = np.random.randn(3,7)
#계층 생성
in_layer0 = MatMul(W_in) #입력층 처리 (맥락 수만큼 생성)
in_layer1 = MatMul(W_in) #가중치 W_in 공유
out_layer = MatMul(W_out)
#순전파
h0= in_layer0.forward(c0)
h1= in_layer1.forward(c1)
h = 0.5*(h0+h1)
s = out_layer.forward(h)
print(s)-> [[-1.8372924 -3.60577232 -3.03437831 -2.01436018 -2.0348912 -1.20465769 -0.26381478]]
=> 각 단어의 점수
3.2.2 CBOW 모델의 학습
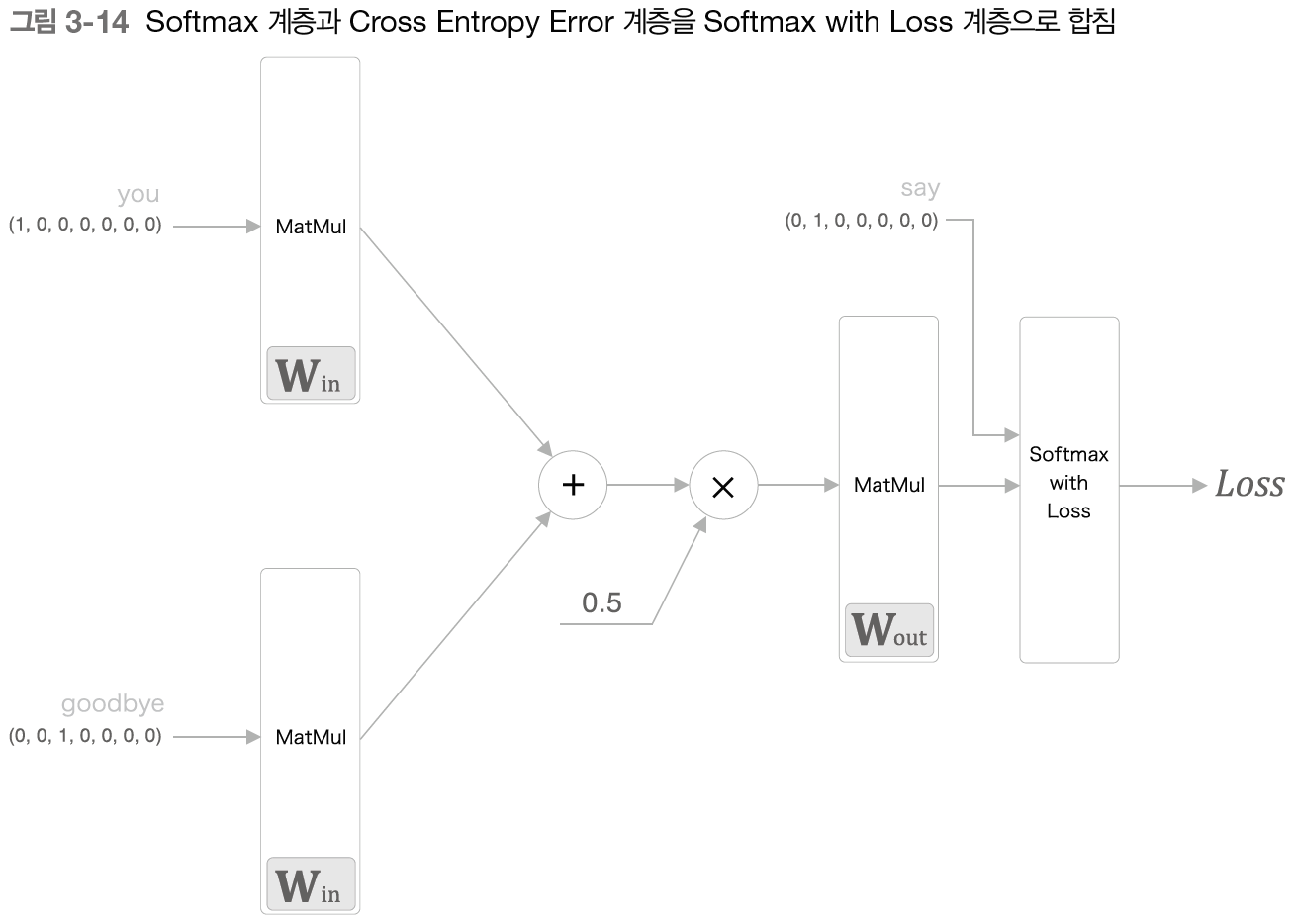
- 다중 클래스 분류 수행하는 신경망
- 소프트맥스 - 점수를 확률로 변환
- 교차 엔트로피 오차 - 확률과 정답 레이블로부터 교차 엔트로피 오차 구함 (손실) -> 학습 진행
3.2.3 word2vec의 가중치와 분산 표현
- 두 가지 가중치
- 입력 측 완전연결계층의 가중치 (W_in) : 각 단어의 분산 표현
- 출력 측 완전연결계층의 가중치 (W_out) : 단어의 의미가 인코딩된 벡터 (열 방향으로 저장)
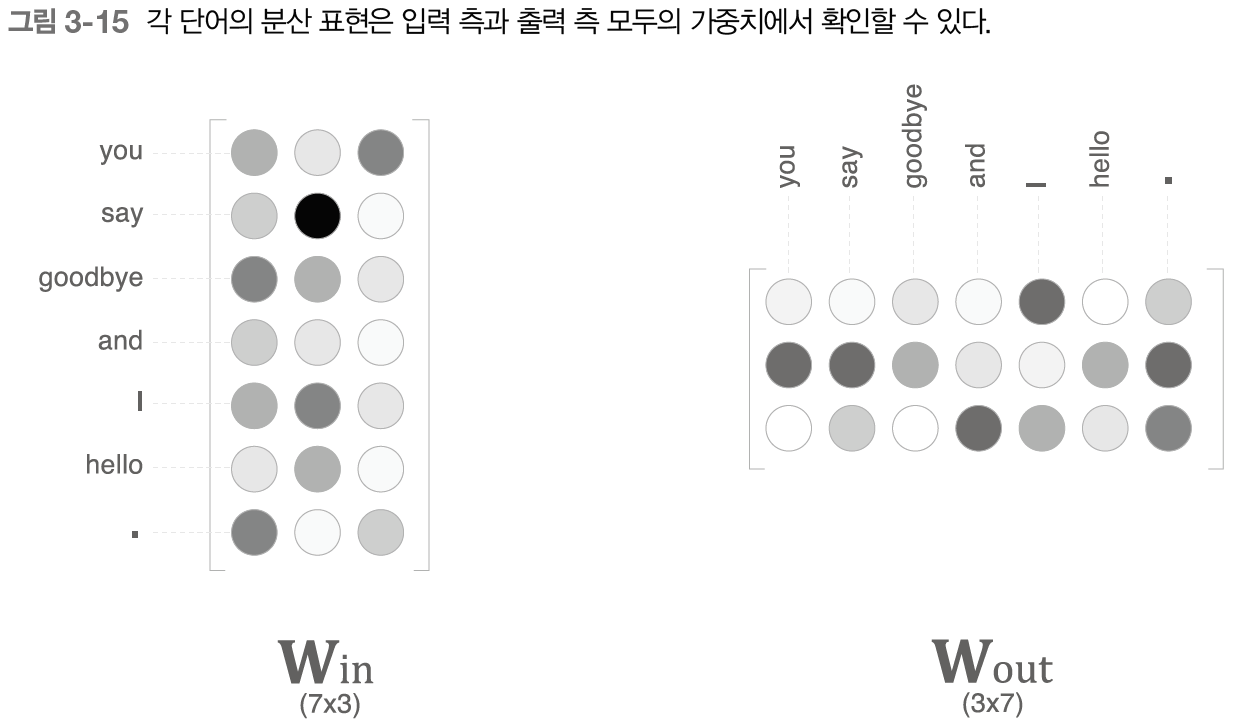
- word2vec에서는 입력 측의 가중치(W_in)을 최종 단어의 분산 표현으로 이용하는 것이 대중적인 선택
3.3 학습 데이터 준비
3.3.1 맥락과 타깃

- 맥락의 각 행이 신경망의 입력
- 타깃의 각 행이 정답 레이블
- 맥락의 수는 여러 개가 될 수 있지만 타깃은 오직 하나

from common.util import preprocess
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text) #말뭉치 텍스트를 단어 ID로 변환
##corpus로부터 맥락과 타깃을 만드는 함수
def create_contexts_target(corpus, window_size=1):
target = corpus[window_size:-window_size] #양끝제외
contexts=[]
for idx in range(window_size, len(corpus)-window_size): #타겟의 인덱스범위
cs = []
for t in range(-window_size, window_size +1): #-1, 0, 1
if t ==0: #타겟일 경우 제외
continue
cs.append(corpus[idx+t]) #타겟의 맥락인덱스
contexts.append(cs)
return np.array(contexts), np.array(target)
##함수 사용
contexts, target = create_contexts_target(corpus, window_size=1)
print(contexts)
print(target)->
[[0 2]
[1 3]
[2 4]
[3 1]
[4 5]
[1 6]]
[1 2 3 4 1 5]맥락과 타깃 - 단어ID로 구성됨
3.3.2 원핫 표현으로 변환

- 단어ID를 이용한 맥락의 형상 (6,2) -> 원핫 표현 (6,2,7)
- 원핫 표현으로의 변환 : convert_one_hot()함수 사용
##원핫 표현으로 변환
from common.util import preprocess, create_contexts_target, convert_one_hot
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text) #말뭉치를 단어 ID로 변환
contexts, target = create_contexts_target(corpus, window_size=1) #맥락과 타깃 얻기
vocab_size = len(word_to_id)
#맥락과 타깃 원핫 표현으로 변환
target = convert_one_hot(target, vocab_size) #단어ID목록과 어휘수 인수로 받음
contexts = convert_one_hot(contexts, vocab_size)3.4 CBOW 모델 구현
- SimpleCBOW 구현

from common.layers import MatMul, SoftmaxWithLoss
class SimpleCBOW:
def __init__(self, vocab_size, hidden_size):
V, H = vocab_size, hidden_size
#가중치 초기화
W_in = 0.01*np.random.randn(V, H).astype('f') #32비트 부동소수점 수로 초기화
W_out = 0.01*np.random.randn(H, V).astype('f')
#계층 생성
self.in_layer0 = MatMul(W_in) #맥락에서 사용하는 단어의 수만큼 입력MatMul계층 만들기(2개)
self.in_layer1 = MatMul(W_in)
self.out_layer = MatMul(W_out)
self.loss_layer = SoftmaxWithLoss()
#모든 가중치와 기울기를 리스트에 모은다.
layers = [self.in_layer0, self.in_layer1, self.out_layer]
self.params, self.grads = [], []
for layer in layers:
self.params += layer.params
self.grads +=layer.grads
#인스턴스 변수에 단어의 분산 표현을 저장
self.word_vecs = W_in
#순전파 메서드 구현
def forward(self, contexts, target):
h0 = self.in_layer0.forward(contexts[:, 0]) #맥락의 첫번째 단어 (6,7)
h1 = self.in_layer0.forward(contexts[:, 1]) #맥락의 두번째 단어 (6,7)
h = (h0+h1) *0.5
score = self.out_layer.forward(h)
loss = self.loss_layer.forward(score, target)
return loss
#역전파 메서드 구현
def backward(self, dout=1):
ds = self.loss_layer.backward(dout)
da = self.out_layer.backward(ds)
da *= 0.5
self.in_layer1.backward(da)
self.in_layer0.backward(da)
return None
3.4.1 학습 코드 구현
##학습 코드 구현
from common.trainer import Trainer
from common.optimizer import Adam
from simple_cbow import SimpleCBOW
from common.util import preprocess, create_contexts_target, convert_one_hot
window_size = 1
hidden_size = 5
batch_size = 3
max_epoch = 1000
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text) #말뭉치를 단어 ID로 변환
contexts, target = create_contexts_target(corpus, window_size=1) #맥락과 타깃 얻기
vocab_size = len(word_to_id)
#맥락과 타깃 원핫 표현으로 변환
target = convert_one_hot(target, vocab_size) #단어ID목록과 어휘수 인수로 받음
contexts = convert_one_hot(contexts, vocab_size)
model = SimpleCBOW(vocab_size, hidden_size)
optimizer = Adam() #매개변서 갱신 방법
trainer = Trainer(model, optimizer)
trainer.fit(contexts, target, max_epoch, batch_size)
trainer.plot()
-> 학습을 거듭할수록 손실이 줄어든다
##학습이 끝난 후의 가중치 매개변수 확인
word_vecs = model.word_vecs
for word_id, word in id_to_word.items():
print(word, word_vecs[word_id])you [ 1.1629325 -0.9632237 1.0220319 -0.9973298 1.7453 ]
say [-0.6323519 1.2298591 0.02795994 1.1977036 1.124968 ]
goodbye [ 0.76684 -0.95298827 1.010701 -0.98307246 -0.8858874 ]
and [-1.5050563 0.99208957 1.668874 0.9707058 0.74477434]
i [ 0.7717827 -0.9794516 1.0309044 -0.99582094 -0.89843786]
hello [ 1.151623 -0.95551836 1.0052384 -0.9810654 1.769742 ]
. [ 1.6542563 1.1570057 -1.4423819 1.1536727 1.1364125]
#가중치 초기화에서 random()함수를 사용하므로 실행할 때마다 결과 달라짐- 단어 ID의 분산 표현 출력
- 단어를 밀집벡터로 나타냄
-> 학습이 잘 이뤄졌기 때문에 단어의 의미를 잘 파악한 벡터 표현 - 처리 효율 면에서 몇 가지 문제 존재
3.5 word2vec 보충
3.5.1 CBOW 모델과 확률
- 동시 확률 : P(A, B) : A와 B가 동시에 일어날 확률
- 사후 확률 : P(A|B) : B가 주어졌을 때 A가 일어날 확률

-> Wt-1과 Wt+1이 주어졌을 때 타깃이 Wt가 될 확률

-> 교차 엔트로피 오차 적용

-> 말뭉치 전체로 확장
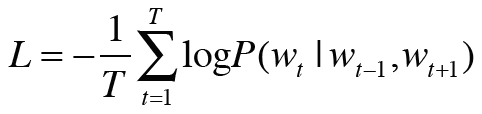
=> 음의 로그 가능도 :CBOW모델의 손실 함수
3.5.2 skip-gram 모델
: CBOW에서 다루는 맥락과 타깃을 역전시킨 모델
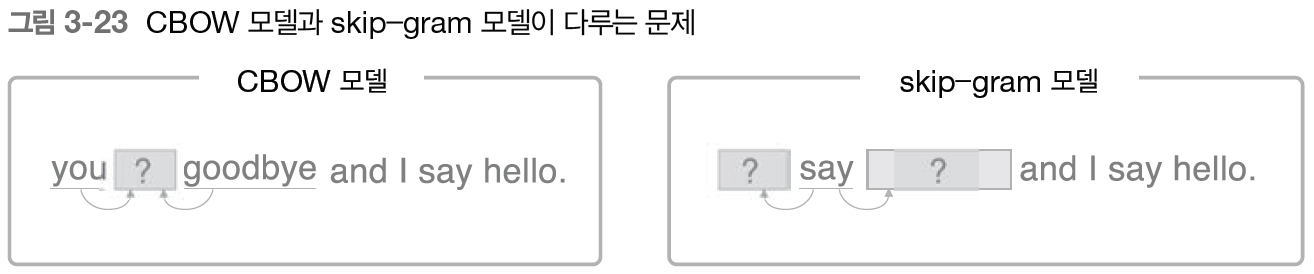
-> 중앙의 단어(타깃)로부터 주변의 여러 단어 (맥락)을 추측

- 입력층은 하나
- 출력층은 맥락의 수만큼 존재
- 출력층에서는 개별적으로 손실을 구하고, 이 개별 손실들을 모두 더한 값이 최종 손실
-> Wt가 주어졌을 때 Wt-1과 Wt+1이 동시에 일어날 확률

-> 맥락 단어들 사이에 관련성이 없다고 가정하고 분해 (조건부 독립)
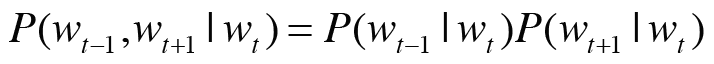
-> 교차 엔트로피 오차 적용

-> 말뭉치 전체로 확장

=> skip-gram모델의 손실 함수
- skip-gram 모델
- 손실 함수는 각 맥락에서 구한 손실의 총합
- CBOW 모델
- 타깃 하나의 손실
=> skip-gram 모델의 단어 분산 표현의 정밀도 면에서 결과가 더 좋음
- 더 어려운 상황에서 단련하기 때문
- 특히 말뭉치가 커질수록 성능이 더 뛰어남
- 학습 속도 면에서는 CBOW 모델이 더 빠름
3.5.3 통계 기반 vs. 추론 기반
- 통계 기반 기법
- 어휘 추가 -> 계산 처음부터 다시
- 주로 단어의 유사성이 인코딩
- 추론 기반 기법
- 매개변수 다시 학습 (기존 학습 가중치는 초깃값으로 사용) -> 효율적 갱신 가능
- 단어의 유사성 + 복잡한 단어 사이의 패턴까지 인코딩
=> 우열을 가리기 힘듦
- 서로 관련되어 있음
- 추론 기반 기법도 말뭉치 전체의 동시발생 행렬에 특수한 행렬 분해를 적용한 것과 같음
- 추론 기반 기법과 통계 기반 기법을 융합한 GloVe기법 등장
말뭉치 전체의 통계 정보를 손실 함수에 도입해 미니배치 학습을 하는 것
3.6 정리
- 추론 기반 기법은 추측하는 것이 목적이며, 그 부산물로 단어의 분산 표현을 얻을 수 있다.
- word2vec은 추론 기반 기법이며, 단순한 2층 신경망이다.
- word2vec은 skip-gram, CBOW 모델을 제공한다.
- CBOW 모델은 여러 단어(맥락)로부터 하나의 단어(타깃)을 추측한다.
- 반대로 skip-gram모델은 하나의 단어(타깃)로부터 다수의 단어(맥락)을 추측한다.
- word2vec은 가중치를 다시 학습할 수 있으므로, 단어의 분산 표현 갱신이나 새로운 단어 추가를 효율적으로 수행할 수 있다.
책 참고 : 밑바닥부터 시작하는 딥러닝 (한빛미디어)
'딥러닝 > 밑바닥부터 시작하는 딥러닝 2' 카테고리의 다른 글
| 6장 : 게이트가 추가된 RNN (0) | 2023.09.26 |
|---|---|
| 5장 : 순환 신경망(RNN) (0) | 2023.09.26 |
| 4장 : word2vec 속도 개선 (0) | 2023.09.23 |
| 2장 : 자연어와 단어의 분산 표현 (2) | 2023.09.21 |
| 1장 : 신경망 복습 (0) | 2023.09.20 |



