통계학의 이해 1 - week6 : 조건부확률

1. 확률의 정리

확률의 기본정리①

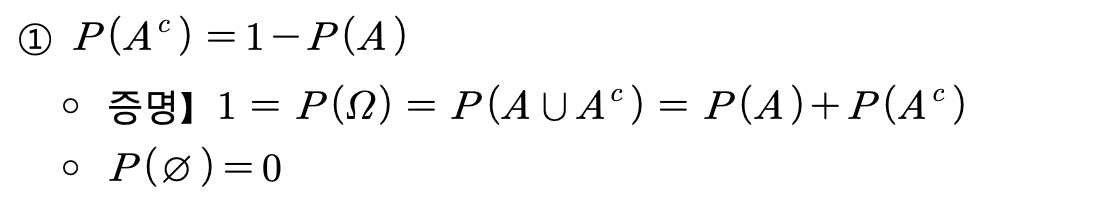
• 예제 ) k명 중 적어도 두 사람 이상이 생일이 같을 확률
  • A = k명의 사람이 모두 다른 생일을 가지는 사건 

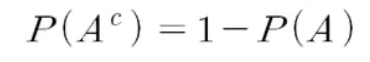
• 예제 ) 1000장 중 4장 당첨복권
  • 4장의 복권을 구입한다면 적어도 한 장 이상의 당첨복권을 구입하게 될 확률은?
  • A : 한 장 이상의 당첨복권을 구입할 사건 = 당첨복권이 한 장, 두 장, 세 장, 네 장인 경우 
  • A 여사건 : 구입한 4장 모두 당첨되지 않을 사건

 

확률의 기본정리②

 

확률의 기본정리③

 

확률의 기본정리④

 

 

 

 

-> 합집합의 상한값

 

 

 

 

-> 교집합의 하한값

 

 

• 예제) 1000장 중 4장이 당첨복권

---

2. 조건부 확률

조건부 확률

: 확률실험에서 새로운 정보 또는 조건(A)이 추가되었을 때, 사건 B의 확률 

• 사건 A가 발생했다면 A 이외의 것은 일어날 수 없음
  -> A가 새로운 표본공간 Ω'이 되고, B가 발생한다는 것은 A∩B에 있는 원소가 발생하는 것을 의미
• 사건 A가 주어졌을 때 사건 B의 조건부 확률

 

예) - 사망률

• 어느 해의 40대 사망률 : 그해 40대 이상인 사람들 중에서 40대에 사망한 사람의 비율 
  • 표본공간이 전체 연령대에서 40대 이상으로 축소
• 생존율 : 40대 이상인 사람 중 그 해 생존한 사람의 비율
  • 생존율 = 1-사망률
• 완전생명표

• 0세 사망자 : 100,000-99709 = 291
  -> 영아 사망률 = 291 / 100000 = 0.29%
• 40세 남성사망률 = 146 / 97727 = 0.00149 = 0.15%
• 80세 여성 생존율 = 72910 / 75732 = 96.7%

 

조건부확률의 활용①

예제 ) 정상제품(정) 90개와 불량품(불) 10개가 들어있는 상자에서 무작위로 2개를 비복원으로 추출

•  Ω = {(정,정), (정,불), (불,정), (불,불)}
• (정,정)의 확률? 
  • 첫번째가 정상일 확률 90/100 -> P(정)
  • 두번째도 정상일 확률 89/99 -> P(정|정)
  • P(정,정) = 90/100 * 89/99 = 89/110

 

조건부확률의 활용②

• 어떤 일련의 사건들이 순차적으로 결합된 경우
  -> 특정 시점에서의 사건 확률은 앞에서 발생할 수 있는 상황이나 연결된 상황들의 확률을 모두 더하여 구할 수 있음

예제 ) 당첨복권이 4장인 복권 1000장 발매

• 2번째 당첨 확률 = (1번째 당첨되고 2번째도 당첨될 확률) + (1번째 당첨안되고 2번째 당첨될 확률)

 

예제 ) 스팸메일 필터

 

표본공간의 분할

                                              -> ∑P(Ai)P(B|Ai)

 

---

3. 독립사건

독립사건

• A와 B가 독립이면 A와 B의 여집합, A여집합과 B, A여집합과 B여집합 모두 독립
• 배반사건 : A∩B = ∮-> 독립x

예) - 두 개의 정육면체 주사위 

   Ω = (1,1) ....(6,6) = 36가지

• B∩C = {(3,4)}
• A∩C = {(3,3)}
• A와 C -> 1/36 ≠ 5/36 * 6/36 => 독립x
• B와 C -> 1/36 = 6/36 * 6/36 => 독립ㅇ

 

예) - 3 개의 주사위 던지기

• 6이 최소한 한번 이상 나올 확률은?
• A : 주사위 눈이 6인 경우가 최소한 한번 이상 나올 사건

                                = 1- 5/6*5/6*5/6 (6이 나오지 않는 사건)

 

예) - 전기전달 시스템

• 직렬 -> 교집합, 병렬 -> 합집합

---

4. 베이즈 정리

베이즈 정리 

• P(B|A)은 순서적으로 볼 때, 대부분 사건 A가 먼저 발생하고 B가 이어 발생하는 상황에 대한 확률
  • A는 원인, B는 결과의 형태를 가짐
    -> 코호트 연구 (Cohort Study) : 전향적 연구 : 원인 -> 결과
  • 원인의 가능성인 P(A) 또는 P(Ac)는 사건 B가 관측되기 이전의 확률 
    => 사전확률 
• 결과를 얻은 상태에서 그 결과가 발생하게 된 원인을 역으로 추정
  -> 사례 - 대조연구 : 후향적 연구 : 결과 -> 원인
  • 결과 B의 관측했을 때 그 원인이 A일 사건의 확률 : P(A|B)
  • 사건 B가 관측된 후의 A의 확률
    -> 사후확률

-> 가장 큰 확률인 Ai를 원인이라고 판단할 수 있음

예) - 암진단

---

정리

1. 

 

2. 

 

3. 

 

4. 

---

참고 강의: https://lms.kmooc.kr/course/view.php?id=6760#section-1